Right Angled Triangles and Pythagoras Property
Right Angled Triangles and Pythagoras Property: Overview
This topic covers concepts, such as, Right Angled Triangles, Hypotenuse of Right Angle Triangles, Right Isosceles Triangles & Basic Properties of Right Isosceles Triangles etc.
Important Questions on Right Angled Triangles and Pythagoras Property
The the side of an isosceles right triangle whose hypotenuses is is ,value of is _____
The hypotenuses of an isosceles right triangle whose side is
For a triangle , , . Find the relation between and
A triangle with three angles and is known as right _____ triangle
The triangle with and is a _____ triangle.
Find the other angles of the triangle with and
State True or False
The hypotenuses of an isosceles right triangle whose side is is .
An isosceles right triangle has angles of and .
In , if . If is , find the value of .
A ladder m long rests against a vertical wall. If the foot of the ladder is m from the foot of the wall, find the distance of the other end of the ladder from the ground.
ABC is a right angled triangle. and Calculate the area of
AD is drawn perpendicular to BC, the base of an equilateral triangle ABC. Given find the length of AD, correct to place of decimal.
All the angles of the right angled triangle are equal to .
P is a point in the interior of a rectangle ABCD. If P is joined to each of the vertices of the rectangle and the lengths PA, PB and PC are respectively, find the length of PD.
In Fig. is acute angle and Show that,
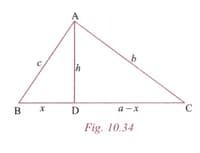
In Fig. is acute angle and Show that,
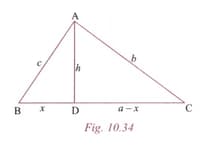
In and D is the mid point of BC. Prove that
In and D is the mid-point of BC. Prove that
In is the mid point of . Prove that
In a right right angled at C, P and Q are points on the sides CA and CB respectively dividing those sides in the ratio
Prove that
